计算机图形学的作业。对凸多边形窗口的线段裁剪Cyrus-Beck算法进行了拓展.
思路
多边形窗口如果是凹多边形,补全为凸多边形窗口组。用每个凸多边形窗口对输入线段进行裁剪,最后线段相减得到结果。
程序流程图
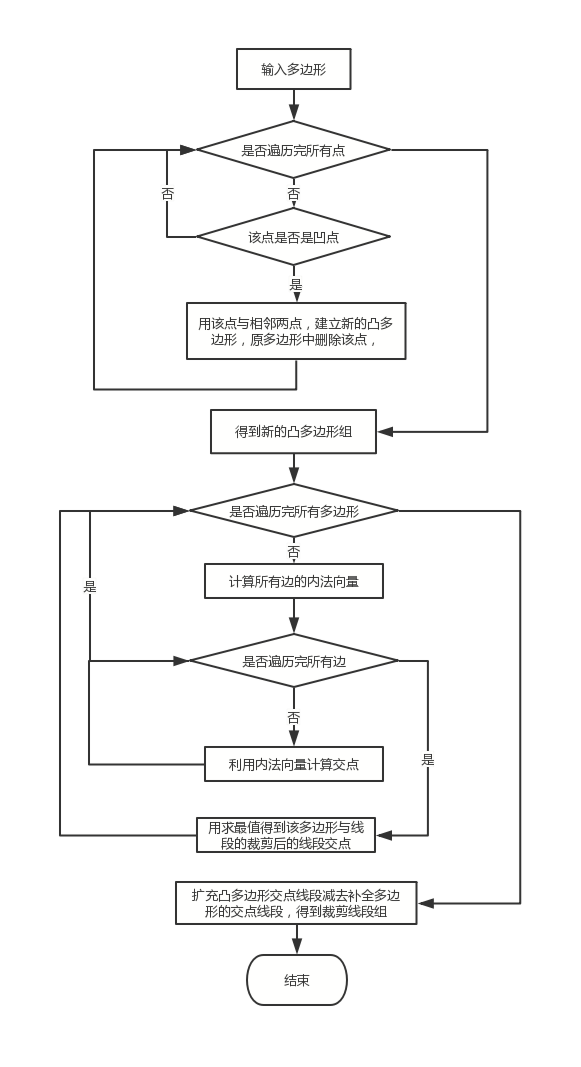
具体实现
利用OpenGL函数库和C++实现了任意多边形窗口的线段裁剪算法。代码开发环境MacOS + Xcode。
自定义数据结构类Polygon多边形,有两个成员变量Point2D数组,分别存储多边形的顶点以及法向量,还有一个成员变量_num存储边的数量。结构中的ComputeNormals()函数计算出内法向量。
1
2
3
4
5
6
7
8
9
| struct Polygon
{
int _num;
Point2D* points;
Point2D* norms;
void Set(vector<Point2D> p){};
void ComputeNormals(){};
}
|
主要函数ComuteLineCross(), 用来找到凹点。输入多边形的点数组p(p的首元素是x坐标值最大的点,依次按边顺序的点数组),并返回凹点在数组中的索引。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| int ComputeLineCross(vector<Point2D> p)
{
int _num = p.size();
Point2D A = p[_num - 1], B = p[0], C = p[1];
float cross = (B._x - A._x) * (C._y - A._y) - (B._y - A._y) * (C._x - A._x);
bool flag = cross < 0;
for(int i = 1; i < _num; ++i)
{
int pre = i - 1 ;
int next = i == _num - 1? 0 : i + 1;
A = p[pre];
B = p[i];
C = p[next];
cross = (B._x - A._x) * (C._y - A._y) - (B._y - A._y) * (C._x - A._x);
if((cross < 0)!= flag)
return i;
}
return -1;
}
|
主要函数generateConvexPolygons(),用来生成补全的凸多边形组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void generateConvexPolygons(vector<Point2D> points, vector<vector<Point2D>>& convexPolygons)
{
int _num = points.size();
int i = ComputeLineCross(points);
if(i == -1)
cout << "The polygen is a concave polygen." << endl;
else
cout << "The polygen is a convex polygen." << endl;
while(i != -1)
{
int pre = i - 1 < 0 ? _num - 1 : i -1;
int next = i + 1 < _num ? i + 1 : 0;
vector<Point2D> p{points[pre], points[i], points[next]};
convexPolygons.push_back(p);
points.erase(points.begin() + i);
_num --;
i = ComputeLineCross(points);
}
convexPolygons.push_back(points);
}
|
主要函数Cyrus_Beck(),用每个凸多边形窗口对原线段进行剪裁。输入需要剪裁的一条线段、一个多边形以及有效线段数组,返回值为-1时代表该线段在多边形外侧,无有效线段,无需剪裁。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| int Cyrus_Beck(Line2D& src, Polygon& poly)
{
float tin = 0.0f, tout = 1.0f;
Point2D&& vec = src.GetVector();
for(int i = 0; i < poly._num; ++i)
{
Line2D&& line = poly.GetLine(i);
Point2D&& norm = poly.GetNormal(i);
float nc = vec * norm;
if(nc == 0)
continue;
else
{
float hit = (line._start - src._start) * norm / nc;
if(nc > 0)
tout = min(tout, hit);
else
tin = max(tin, hit);
}
}
if(tin <= tout)
{
Line2D dest_T;
dest_T._start = src._start + vec * tin;
dest_T._end = src._start + vec * tout;
dest_V.push_back(dest_T);
}
return tin > tout;
}
|
实验结果
程序运行后,先用鼠标左键选取一系列的点,单击鼠标右键完成多边形的构建。接下来用鼠标左键选取线段的起点和终点进行裁剪。

图1 凸多边形窗口裁剪线段结果

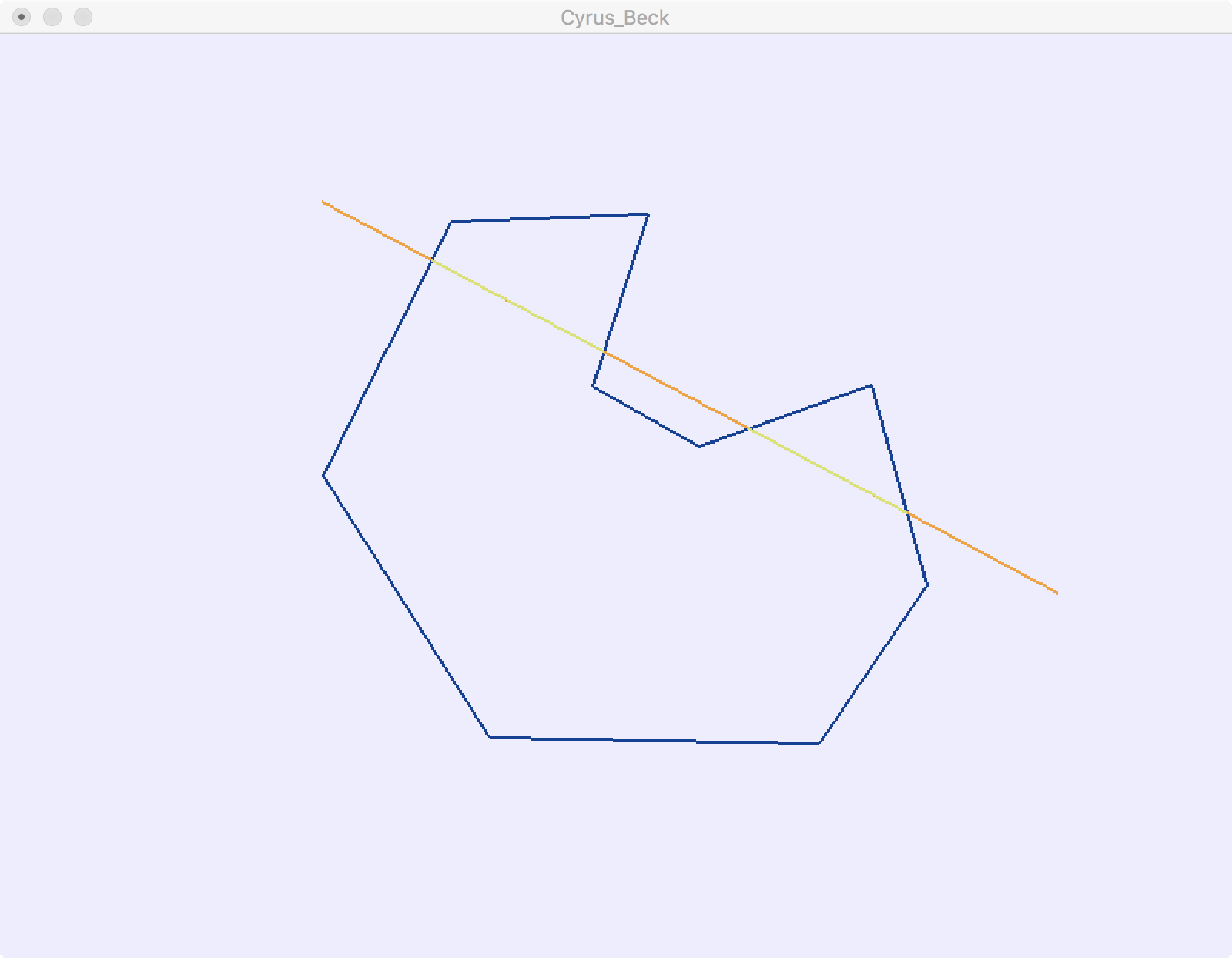
图2 凹多边形窗口裁剪线段结果