数据库课上要讲的图数据论文《Adaptive Asynchronous Parallelization of Graph Algorithms》。提出了一种新的图系统的并行模型AAP,并进行了实验验证。
《Adaptive Asynchronous Parallelization of Graph Algorithms》 SIGMOD’18
To: Wenfei Fan, Ping Lu, et. al.
From: University of Edinburgh
简介
本文对图计算任务提出了AAP(自适应异步并行)模型。
相比于BSP(Bulk Synchronous Parallel整体同步并行)模型和AP(Asynchronous Parallel异步并行)模型,AAP模型通过动态调整工作进程worker的相对进度,减少了很多杂乱无章的计算。
BSP, AP和SSP(Stale Synchronous Parallel过时异步并行)模块都是AAP的特殊案例。更好的是,AAP模块能在单次执行的不同阶段中自适应地在这些模型间切换,优化并行处理。
并且,通过采用GRAPE的编程模型,AAP目的是基于定点计算以及部分评估和增量评估来并行化现有的顺序算法。在单调条件下,如果顺序算法正确,则AAP能保证收敛于正确答案。
此外,作者证明了AAP能够最佳模拟MapReduce,PRAM,BSP,AP和SSP。
通过在真实场景图和合成图上的实验,验证了AAP在各种图形计算方面地性能均优于BSP,AP和SSP。
相关工作和对比分析
参数同步模式
参数同步有BSP、ASP、SSP三种模式。
BSP模型用在一些图系统里,比如Prefel和GRAPE。
BSP模型的迭代计算由一系列串行的超步组成,只有下一个超步才能访问这个超步得到的信息。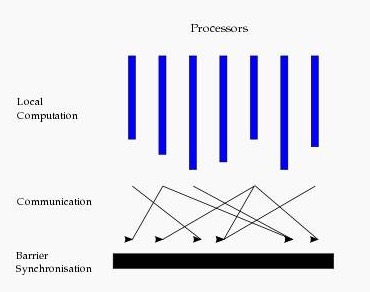
每一个超步中,分为3个阶段
- 本地计算阶段:在本地的计算
- 全局通信阶段 :每个worker之间的数据的交流,即每个worker拿到不在本地的数据的阶段
- 栅栏同步阶段:是一个类似与栅栏的装置,使得已经完成的进程等待其它的进程结束
这种方法优势在于每一个worker下次开始都能拿到最新的全局参数,意味着同步迭代质量很高。 但是,它的global synchronization barrier会导致Straggler问题,也就是说如果有某个worker比其他worker计算得慢很多,每个超步的速度都会被限制为最慢的worker的速度。
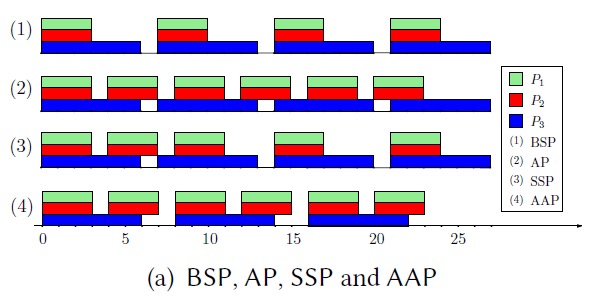
为了解决Straggler问题,GraphLab和Maiter等图系统采用了异步并行(AP)模型。AP模型中没有同步,因此快的worker无需等待其他worker就能继续执行。这种情况可能导致过时计算问题。比如图a中(2)的P1和P2迭代完5次,只能拿到P3的迭代第2次的信息。
过时计算通常增加了不必要的计算和通信成本。而且如果异构性很强,计算可能会不收敛。
对于很多图算法,为了优化性能,单次执行的不同阶段需要不同的模型。因此提出了SSP和Hsynv。
SSP优势在BSP和ASP之间进行折中,一定程度上兼顾了迭代质量和迭代速度,只让最快的worker比最慢的worker快一个固定的步数。SSP因此减少了straggler问题,但是会导致多余的过时计算。
Hsync在AP和BSP之间切换,但是需要预测切换点,会造成预测开销和切换开销。
贡献点
能不能有一个简单的并行模型来继承BSP和AP的优点,并减少散乱和过时的计算,而无需在两者之间进行明确切换? 因此作者提出了AAP,同时保留BSP编程,确保一致性并能保证正确的收敛?
由于没有全局同步障碍,AAP本质上是异步的。
与BSP和AP不同,AAP的每个worker都有两个测量参数:
(a)相对于其他worker的进度
(b)过时消息的积累
每个worker都可以立即访问传入的消息,并根据自己的参数决定是否启动下一轮计算。与SSP相比,每个worker能根据自己的相对进度和消息滞后性动态调整自己的参数,而不需要一个固定约束.
大纲
Programming model。介绍GRAPE编程模型
AAP。
证明了BSP, AP和SSP(Stale Synchronous Parallel过时异步并行)模块都是AAP的特殊案例。不仅如此,AAP模块能在单次执行的不同阶段中自适应地在这些模型间切换,优化并行处理。Foundation
本文将AAP建模为具有部分评估和增量计算的同步定点计算(第4节)。我们提供条件让AAP能保证收敛和Church-Rosser属性。我们还表明,AAP可以最佳模拟MapReduce,PRAM,BSP,AP和SSP。AAP Programming
展示了可以通过AAP轻松进行各种图形计算(第5节)。这些包括最短路径(SSSP),连接的组件(CC),协作过滤(CF)和PageRank(PageRank)。Implementation
我们通过将GRAPE [23]从BSP扩展到AAP(第6节)来开发GRAPE +.Experiments
与表1中列出的最新图形系统以及SSP下的参数服务器Petuum相比,我们使用现实生活中的综合图来评估GRAPE +(第7节)的性能。